[Baekjoon] 단계별로 풀어보기 : 약수, 배수와 소수

자료구조와 알고리즘/문제풀이

[Baekjoon] 단계별로 풀어보기 : 약수, 배수와 소수

순정법사 2023.08.25

이번 알고리즘 문제 풀이는 C로 진행했습니다

코드에 오탈자나 문제가 있으면 언제든지 댓글로 알려주세요!

A. 약수, 배수와 소수

약수, 배수와 소수 단계

약수를 구하면서 주어진 수가 완전수인지 판별하는 문제

www.acmicpc.net

1. 배수와 약수

a. 문제지 : 5086

b. 풀이

입력은 여러개의 테스트 케이스로 이루어져 있다 = 입력을 반복문으로 받아야 함

c. 정답

📚 풀이

#include <stdio.h>

int main() {
    while (1) {  // 무한 루프 시작
        int A, B;
        scanf("%d %d", &A, &B);

        if (A == 0 && B == 0)
            break;  // 입력이 0 0이면 루프 종료

        // 첫 번째 숫자가 두 번째 숫자의 약수인지 확인
        if (B % A == 0) {
            printf("factor\n");
        } 
        // 첫 번째 숫자가 두 번째 숫자의 배수인지 확인
        else if (A % B == 0) {
            printf("multiple\n");
        } 
        // 둘 다 아니라면
        else {
            printf("neither\n");
        }
    }  // 무한 루프 종료

    return 0;
}

2. 약수 구하기

a. 문제지 : 2501

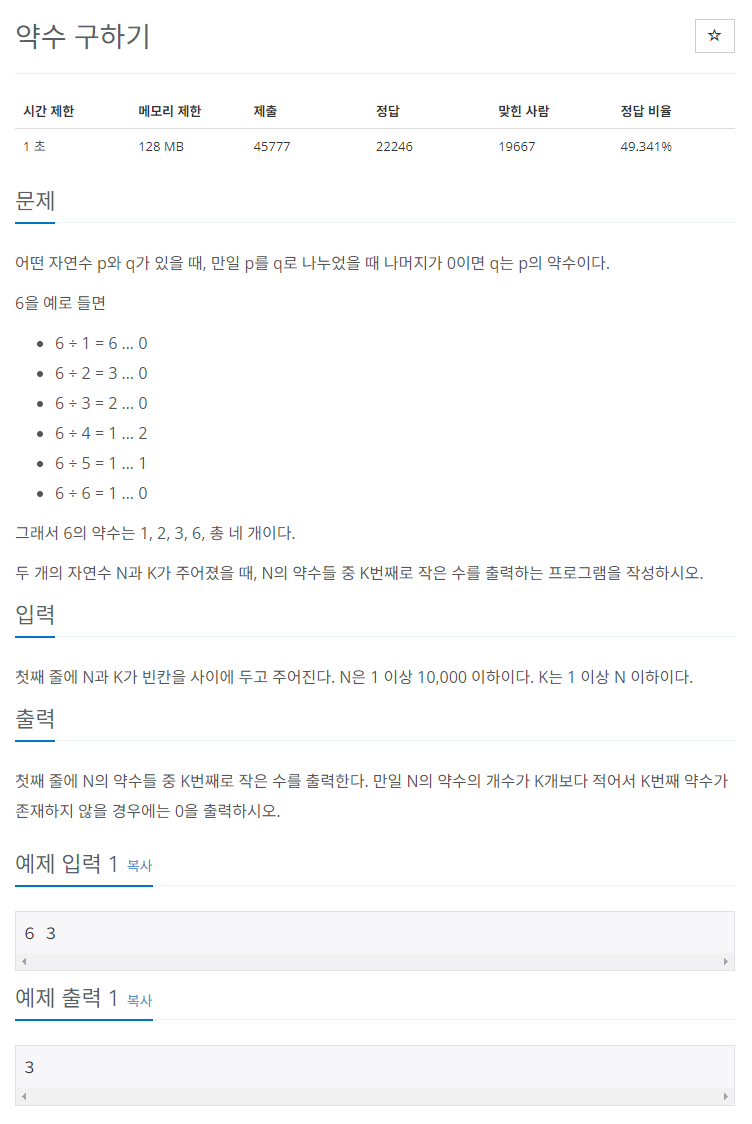
b. 알고리즘 / 풀이

풀이 1) 약수의 순서를 K와 비교하며 출력

자연수 N과 K를 입력
약수의 개수를 저장하는 변수 count를 초기화
약수를 저장할 변수 i를 초기화
1부터 N까지 반복
a) N % i == 0인지 (약수인지) 확인하고 맞다면 count를 증가
만약 count가 K와 같아지면 반복문 종료
b) 약수가 아니라면, 아무일도 일어나지 않음
반복문이 종료된 후 결과 출력
a) 원하는 순서의 약수를 찾거나 (count ==K) , i가 N보다 작을 때 (i <= N, 약수를 못찾은 경우 위 반복문에서 i가 N보다 커짐) i를 출력
b) 그 이외의 경우는 K번째 약수가 존재하지 않으므로 0을 출력

풀이 2) 찾은 약수를 배열에 저장 후 K 번째 약수를 찾기

N과 K를 입력
factors 배열을 선언하여 약수를 저장
count 변수를 초기화
1부터 N의 제곱근까지 반복하면서 약수를 찾음
N을 i로 나누었을 때 나머지가 0인 경우 i는 N의 약수 = i를 factors 배열에 저장
i가 N의 제곱근이 아닌 경우에는 N을 i로 나눈 값을 또 저장
factors 배열을 qsort 함수를 이용해 오름차순으로 정렬
K가 count보다 작거나 같은 경우, factors 배열에서 K번째 약수를 출력
아니면 K번째 약수가 없다는 의미로 0을 출력

🧡 약수는 항상 한 쌍

약수는 항상 한 쌍을 이룸 ( ex. 6 = 1*6 / 2*3 )
따라서 알고리즘에서 sqrt(N) : (N의 제곱근) 을 사용하는 이유는
약수를 구할 때 1부터 N까지 모든 수를 검사하는 것이 아니라 1부터 sqrt(N)까지만 검사해도 충분함!!

c. 정답

📚 풀이 1 : K번과 약수 순서를 비교하며 풀이

#include <stdio.h>
 
int main() {
    int N, K;  // 자연수 N과 K를 저장할 변수
    scanf("%d %d", &N, &K);  // N과 K를 입력 받음
    
    int cnt = 0;  // 약수의 개수를 저장할 변수
    int i = 0;
    
    //N까지 반복하면서 약수를 찾음
    //i++때문에 K번째 약수까지 못 찾은 경우 i가 N보다 1 커지기 때문에
    //if(i<=N) 조건문이 성립하지 않음
    for (i = 1; i <= N; i++) {	
        if (N % i == 0)  // i가 N의 약수인 경우
            cnt++;  // 약수의 개수를 증가시킴
        
        if (cnt == K)  // K번째 약수를 찾은 경우
            break;  // 반복문을 종료
    }
    
    //원하는 순서의 약수를 찾거나, i가 N보다 작을 때 
    if (cnt == K){ // or (i<=N)도 가능
        printf("%d", i);  // K번째 약수 출력
    }else{
        printf("0");  // K번째 약수가 없을 경우
    }
    
    return 0;
}

[BaeKJoon/C] 백준2501 c 약수 구하기

https://www.acmicpc.net/problem/2501 2501번: 약수 구하기 첫째 줄에 N과 K가 빈칸을 사이에 두고 주어진다. N은 1 이상 10,000 이하이다. K는 1 이상 N 이하이다. www.acmicpc.net 문제 어떤 자연수 p와 q가 있을 때,

succeeed3256.tistory.com

📚 풀이 2 : 찾은 약수를 배열에 저장 후 K 번째 약수를 찾아 풀이

#include <stdio.h>
#include <math.h>
#include <stdlib.h>

// 비교 함수
int compare(const void *a, const void *b) {
    return (*(int *)a - *(int *)b);
}

int main() {
    int N, K;
    scanf("%d %d", &N, &K);  // N과 K를 입력 받음
    
    int factors[10000]; // 약수를 저장할 배열
    int count = 0;  // 약수의 개수를 저장할 변수

    // 1부터 N의 제곱근까지 반복하여 약수를 찾음
    for (int i = 1; i <= sqrt(N); i++) {
        if (N % i == 0) {  // i가 N의 약수인 경우
            factors[count++] = i;  // 약수를 배열에 저장

            if (i != N / i) {  // i가 N의 제곱근이 아닌 경우
                factors[count++] = N / i;  // N을 i로 나눈 값도 약수이므로 배열에 저장
            }
        }
    }
    
    // qsort 함수를 이용해 배열을 오름차순으로 정렬
    //배열의 주소, 요소의 개수, 요소의 크기, 비교 함수를 인자로 받아 배열을 정렬
    qsort(factors, count, sizeof(int), compare);

    if (K <= count) {
        printf("%d", factors[K - 1]);  // K번째 약수 출력
    } else {
        printf("0");  // K번째 약수가 없을 경우
    } 
 
    return 0;
}

3. 약수들의 합

a. 문제지 : 9506

b. 정답

📚 풀이

#include <stdio.h>

int main() {
    while (1) {  // 무한 루프
        int N;
        scanf("%d", &N);  // 사용자로부터 정수 N을 입력 받음
        
        if (N == -1) {  // N이 -1인 경우 루프 종료
            break;
        }
        
        int fac[10001];  // 약수를 저장할 배열
        int count = 0, sum = 0;  // 약수 개수와 약수의 합을 저장할 변수
        
        // 1부터 N의 직전 값까지 반복하면서 약수를 찾음
        for (int i = 1; i < N; i++) {
            if (N % i == 0) {  // i가 N의 약수인 경우
                sum += i;  // 약수의 합을 계산
                fac[count++] = i;  // 약수를 배열에 저장
            } 
        }
        
        if (sum == N) {  // 약수의 합이 N과 같은 경우 (완전수인 경우)
            printf("%d = ", N);  // 완전수의 표시 출력
            for (int i = 0; i < count; i++) {
                if (i == (count - 1)) {  // 마지막 약수인 경우
                    printf("%d\n", fac[i]);  // 약수 출력
                } else {
                    printf("%d + ", fac[i]);  // 약수와 "+" 출력
                }
            }
        } else {  // 완전수가 아닌 경우
            printf("%d is NOT perfect.\n", N);  // 완전수가 아님을 표시
        }
    }
    
    return 0;  // 프로그램 종료
}

4. 소수 찾기

a. 문제지 : 1978

b. 정답

📚 풀이

#include <stdio.h>

int main() {
    int N;  // 테스트 케이스 개수를 저장할 변수
    scanf("%d", &N);  // 테스트 케이스 개수 입력 받음
    int count = 0;  // 소수의 개수를 저장할 변수
        
    while (N--) {  // 테스트 케이스 개수만큼 반복
        int num;  // 입력 받을 정수를 저장할 변수
        scanf("%d", &num);  // 정수 입력 받음
        
        if (num <= 1) {
            continue;  // 1 이하의 수는 소수가 아니므로 건너뜀
        }

        for (int i = 1; i < num; i++) {
            if ((i + 1) == num) {  // i+1이 num과 같은 경우 (소수인 경우)
                count++;  // 소수 개수를 증가시킴
            } else if (num % (i + 1) == 0) {  // num을 (i+1)로 나누어 떨어지는 경우 (소수가 아닌 경우)
                break;  // 루프 종료 (더 이상 소수 확인 필요 없음)
            }
        }
    }
    
    printf("%d\n", count);  // 총 소수의 개수 출력
    return 0;  // 프로그램 종료
}

5. 소수

a. 문제지 : 2581

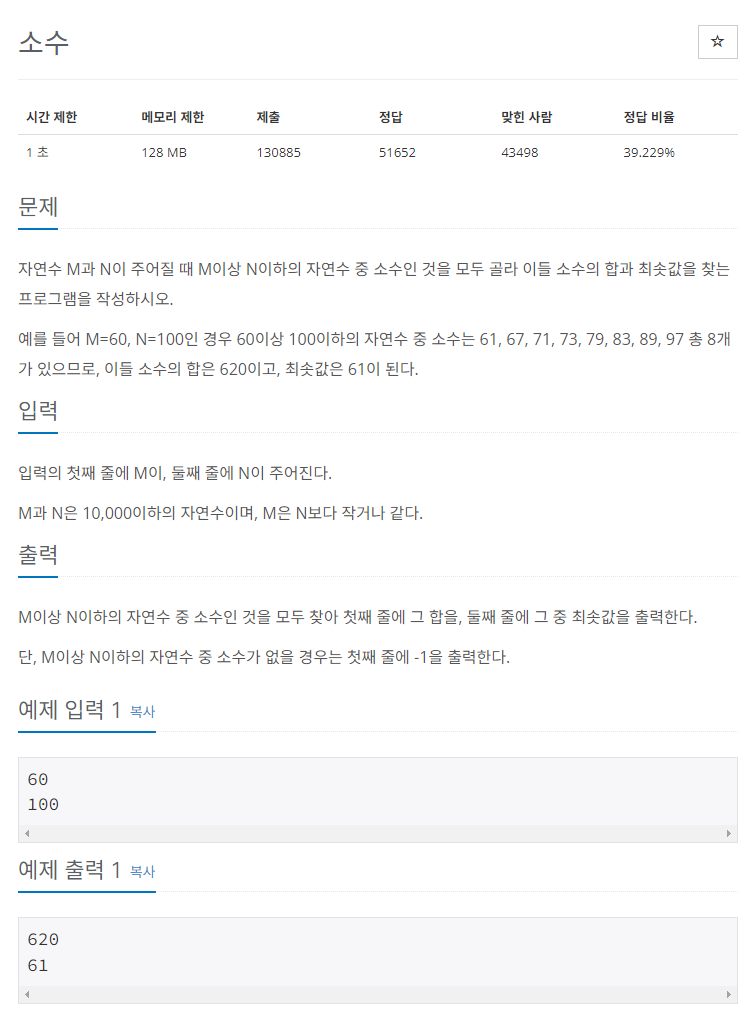
b. 알고리즘 / 풀이

M과 N 입력
소수의 합을 저장할 변수 sum을 초기화
소수 중 최솟값을 저장할 변수 min을 큰 값으로 초기화
M부터 N까지의 각 수에 대해 아래 과정을 수행
a) 해당 수가 1보다 작거나 같은 경우, 소수가 아니므로 다음으로 넘어감
b) 해당 수가 소수인지 판별하기 위해 2부터 해당 수의 제곱근까지의 모든 수를 검사
c) 어떤 수로 나누어 떨어진다면 해당 수는 소수가 아니므로 is_prime 변수를 0으로 설정하고 루프를 종료
d) 소수인 경우 is_prime 변수는 그대로 1로 유지되고, sum에 해당 수를 더하고 min 값을 갱신
sum 값이 0인 경우는 소수가 없는 경우이므로 "-1"을 출력
아니면 sum과 min 값을 출력

c. 정답

📚 풀이

#include <stdio.h>
#include <math.h>

int main() {
    int M, N;    // M이상 N이하의 자연수
    scanf("%d", &M); 
    scanf("%d", &N); 
    
    int sum = 0;  // 소수의 합을 저장할 변수
    int min = 10001;  // 소수 중 최솟값을 저장할 변수
    
    // M부터 N까지의 각 수에 대해 소수 여부를 판별하고 합과 최솟값을 계산
    for (int num = M; num <= N; num++) {
        int is_prime = 1;  // 소수 여부를 판단하는 변수
        
        if (num <= 1) {  // 1보다 작거나 같은 수는 소수가 아니므로 건너뜀
            continue;
        }
        
        // 소수 판별
        for (int divisor = 2; divisor <= sqrt(num); divisor++) {
            if (num % divisor == 0) {
                is_prime = 0;
                break;
            }
        }
        
        if (is_prime) {  // 소수인 경우 합과 최솟값 갱신
            sum += num;
            if (num < min) {
                min = num;
            }
        }
    }
    
    if (sum == 0) {
        printf("-1\n");  // 소수가 없는 경우
    } else {
        printf("%d\n%d\n", sum, min);  // 소수의 합과 최솟값 출력
    }
    
    return 0;  
}

6. 소인수분해

a. 문제지 : 11653

b. 알고리즘 / 풀이

N입력
N이 1이 될 때까지 아래 과정을 반복
a) 2부터 N의 제곱근까지의 모든 수를 검사
b) 만약 현재 검사하는 수로 N을 나누어 떨어진다면, 해당 수는 N의 소인수이므로 출력하고 N을 해당 수로 나눔
c) N을 나누어 떨어지게 만든 소인수로 나누어 떨어지지 않을 때까지 반복
N이 1이 아닌 경우, N은 소수인 경우이므로 N을 출력

c. 정답

📚 풀이

#include <stdio.h>
#include <math.h>

int main() {
    int N;
    scanf("%d", &N); 
    
    for (int i = 2; i <= sqrt(N); i++) {
        while (N % i == 0) {
            printf("%d\n", i);  // 소인수 출력
            N /= i;
        }
    }
    
    if (N > 1) {
        printf("%d\n", N);  // 마지막 소인수 출력 (N이 1보다 큰 경우)
    }
    
    return 0;  
}

'자료구조와 알고리즘 > 문제풀이' 카테고리의 다른 글

[Baekjoon] 단계별로 풀어보기 : 기하 직사각형과 삼각형 (0)	2023.08.25
[Baekjoon] 단계별로 풀어보기 : 일반 수학 1 (0)	2023.08.25
[Baekjoon] 단계별로 풀어보기 : 2차원 배열 (0)	2023.08.25
[Baekjoon] 단계별로 풀어보기 : 심화 1 (0)	2023.08.24
[Baekjoon] 단계별로 풀어보기 : 문자열 (0)	2023.08.17

현재글[Baekjoon] 단계별로 풀어보기 : 약수, 배수와 소수

게임 개발 스킬트리